Das Wissen, das Du jetzt brauchst!
Die neue Version 18 bietet völlig neue Möglichkeiten für Schachtraining und Analyse: Stilanalyse von Spielern, Suche nach strategischen Themen, Zugriff auf 6 Mrd. LiChess-Partien, Download von chess.com mit eingebauter API, Spielervorbereitung durch Abgleich mit LiChess-Partien, eingebaute Cloud-Engine u.v.m..
Expeditionen in die Schachwelt
von Professor Dr. Christian Hesse
 |
Ultimately chess is just chess - not the best |
|
thing in the world and not the
worst thing in the world, but there is nothing quite like it.
W.C. Fields |
Ein mathematisches Schachbrett-Paradox
2008 wurde vom deutschen Wissenschaftsminister zum „Jahr der Mathematik“ erklärt. 2008 fand in Deutschland allerdings auch eine Schachweltmeisterschaft und die Schacholympiade statt, weshalb man sich 2008 auch als „Jahr des Schachs“ vorstellen könnte. Mehr als Grund genug, um sich ein interessantes Problem anzuschauen, das diese beiden intellektuellen Aktivitäten berührt: Mathematik und Schach. Es handelt sich dabei um ein faszinierendes Paradox, das zu beweisen scheint, dass 64 gleich 65 ist. Dabei zerlegt man ein Schachbrett (das natürlich aus 64 Feldern besteht) in vier Teile und macht aus diesen Teilen ein Rechteck, dessen Seiten auf 5 bzw. 13 Feldern bestehen (was natürlich zu einer Fläche von 5 x 13 = 65 Feldern führt).
Dabei habe ich Folgendes vor Augen:
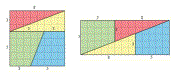
Mit drei geraden Schnitten wurde das Schachbrett in zwei gleiche Dreiecke und zwei gleiche Trapeze geteilt. Die Summe der Flächen dieser vier Teile ergibt 64 kleine Felder auf dem Schachbrett. Diese vier geometrischen Figuren der Zerlegung des Schachbretts können nun zu folgendem Rechteck neu zusammengesetzt werden.
Damit haben wir bewiesen, dass 64 = 65!
Natürlich ist das nicht der Fall und irgendwo muss es einen Fehler geben. Wissen Sie, wo er steckt?
Der Schlüssel für dieses Paradox liegt in Zeichenungenauigkeiten der Linien, aus denen die Dreiecke und die Trapeze und damit auch das Rechteck bestehen. Bei höherer Auflösung gezeichnet sollte das obige Diagramm wie folgt aussehen:
Und wann man den Innenbereich vergrößert, dann sieht man die Kluft zwischen den oberen und unteren Teilen sogar noch deutlicher:
Fn · Fn = Fn(Fn-1 + Fn-2) = Fn · Fn-1 + Fn · Fn-2
und
Fn+1 · Fn-1 = (Fn + Fn-1)Fn-1 = Fn · Fn-1 + Fn-1 · Fn-1
Die in den obigen Diagrammen rot hervorgehobene Fläche hat die Form eines sehr langen Parallelogramms. Es ist verantwortlich für den Flächenunterschied zwischen dem Quadrat und dem Rechteck.
Ein ähnliches Zerlegungsparadoxon ergibt sich, wenn man von einem 13x13-Quadrat ausgeht und die zwei Dreiecke und zwei Trapeze, aus denen es besteht, so neu zusammenfügt, dass, ähnlich wie oben, ein 21x8 Rechteck entsteht:
Erneut sehen wir bei höherer Auflösung folgendes:
Die rot markierte Fläche ist wieder ein Parallelogramm der Fläche 1, bei der sich dieses Mal das obere und das untere Teil überschneiden. So gibt es hier keine Kluft, aber durch die Überschneidung hat das entstehende Rechteck eine kleinere Fläche (=168) als das ursprüngliche Quadrat (=169).
Was ist der mathematische Kern dieses Paradoxons? Um das allgemein zu erklären, beginnen wir mit dem Verweis auf die Folge der so genannten Fibonacci-Zahlen Fn. Dies ist eine Folge von Zahlen, in denen jede Zahl Fn+1 als Summe der beiden Zahlen Fn und Fn-1 vor ihr definiert wird. Deshalb:
Fn+1 = Fn + Fn-1 für n = 1, 2, 3, …
Die Anfangswerte sind durch F0 = 0 und F1 = 1 vorgegeben. So ergeben sich folgende Anfangswerte der Fibonacci-Folge:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, …
Das obige Zerlegungsparadox scheint somit zu sagen, dass
Fn . Fn gleich Fn+1 . Fn-1
Führen wir ein paar einfache Rechnungen durch, um zu sehen, was wirklich passiert:
Fn . Fn = Fn(Fn-1 + Fn-2) = Fn . Fn-1 + Fn . Fn-2
und
Fn+1 . Fn-1 = (Fn + Fn-1)Fn-1 = Fn . Fn-1 + Fn-1 . Fn-1
Die Differenz Dn zwischen diesen beiden Produkten beträgt:
Dn = Fn+1 . Fn-1 - Fn . Fn
= Fn-1 . Fn-1 - Fn . Fn-2
= -Dn-1 = (-1)2 Dn-2 = ... = (-1)n-1D1 = (-1)n
da D1 = F2 . F0 – F1 . F1 = 1 . 0 – 1 . 1 = (-1)1.
Damit haben wir die Wahrheit dessen festgestellt, was als Identität von Cassini bekannt ist:
Fn+1 . Fn-1 – Fn . Fn = (-1)n
Die Schlussfolgerung lautet: Man kann ein Fn x Fn –Quadrat immer in ein Fn+1 x Fn-1 –Rechteck verwandeln und der Unterschied zwischen ihren Flächen Fn . Fn bzw. Fn+1 . Fn-1 beträgt (-1)n , das heißt entweder -1 oder +1. Im ersten Fall überschneiden sich die Teile. Im zweiten Teil gibt es eine Kluft zwischen ihnen.
Das nächst größere Quadrat, bei dem die Zerlegung funktioniert, ist ein 21x21-Quadrat, das wie oben in ein 34x13-Rechteck verwandelt werden kann. Wenn Sie herausfinden wollen, wie das 21x21-Quadrat geschnitten werden muss, denken Sie einfach an die Fibonacci-Folge.
Über den Autor
Christian Hesse hat
an der Harvard University promoviert und war bis 1991 Fakultätsmitglied der
University of California in Berkeley. Seitdem ist er Professor für
Mathematik an der Universität Stuttgart. Nachfolgend war er Gastprofessor
und Gastdozent an Universitäten in der ganzen Welt, von der Australian
National University in Canberra bis zur Universität in
Concepcion-Universität in Chile. Vor kurzem veröffentlichte er das Buch
“Expeditionen in die Schachwelt” ISBN 3-935748-14-0), eine Sammlung von
ungefähr 100 Essays, die der Wiener Standard eines “eines der geistreichsten
und lesenswertesten Bücher, die je über das Schachspiel verfasst wurden”
nannte.
Christian Hesse ist verheiratet, hat eine sechs Jahre alte Tochter sowie
einen zwei Jahre alten Sohn und lebt in Mannheim.
Ihm gefällt Voltaires Antwort, als sich jemand einmal bei ihm beklagte: ”Das
Leben ist hart.” - “Verglichen womit?”
Bisherige Artikel:
Ein großer Moment im Schach...
Ein großer
Moment im Schach (II)...
Ein großer
Moment im Schach (III)...
Ein großer
Moment im Schach (IV)...
Humor im
Schach...
Expeditionen in die Schachwelt: "Schach: Das ultimative unsichtbare Spiel"...
Schach ist vollkommener als das Leben...
